単回帰分析
anscombeデータセットを用いた、単回帰分析を行う。
import seaborn as sns
anscombe = sns.load_dataset('anscombe')
print(anscombe)
出力の一部は下記のとおり。
dataset x y
0 I 10.0 8.04
1 I 8.0 6.95
2 I 13.0 7.58
3 I 9.0 8.81
4 I 11.0 8.33
5 I 14.0 9.96
6 I 6.0 7.24
7 I 4.0 4.26
8 I 12.0 10.84
9 I 7.0 4.82
10 I 5.0 5.68
11 II 10.0 9.14
anscombeデータセットは、4つのデータセットがまとまったものなので、ここではデータセットIを使用する。matplotlibを使用して散布図を描く。
%matplotlib inline
from matplotlib import pyplot as plt
dataset1 = anscombe[anscombe['dataset'] == 'I']
plt.scatter(dataset1['x'], dataset1['y'])
$x$が増加すると$y$も増加するという正の相関が見える。
さらに、直線関係も見えるため(線形)、$y=ax+b$という一次式をあてはめ、係数$a$と切片$b$を求める。
$x$の値が分かれば$y$の値を予測することができるようになる。
上記の一次式で求めた値が予測値であることを示すため、$\hat{y}$のように表現する。
$\hat{y}$は予測値、実際に測定した$y$を実測値とすると、$\epsilon=y-\hat{y}$で求めた実測値と予測値の差$\epsilon$を求めることができる。これを残差という。
残差は正負どちらの値を取ることもあるため、$\epsilon^2$のように二乗した上で、データセットのすべての値についての残差を合計した残差平方和(residual sum of squares)を求める。
$$
Q = \sum_{i=1}^{n}\epsilon_i^2 = \sum_{i=1}^{n}(y_i-(ax_i+b))^2
$$
$Q$を最小にする$a$と$b$を求めるために、最小二乗法を用いることができる。
scikit-learnでは、最小二乗法を用いた線形回帰分析を下記のように行う。
from sklearn import linear_model
x = dataset1['x'].values # numpy.ndarrayに変換
x = x.reshape(-1, 1) # 2次元データに変換、-1はデータに沿って値を決めることを示す
y = dataset1['y'].values
y = y.reshape(-1, 1)
# 線形回帰
model = linear_model.LinearRegression()
model.fit(x, y)
係数$a$と、切片$b$は、下記のようになる。
print('係数: %s' % model.coef_)
print('切片: %s' % model.intercept_)
係数: [[0.50009091]]
切片: [3.00009091]
つまり、下記の回帰式が得られたことになる。
$$
y = 0.5001x+3.0001
$$
先ほどの実測値の散布図に、回帰式の直線を描くと下図のようになる。
import numpy as np
plt.scatter(x, y)
x_for_pred = np.linspace(0, 15)
y_pred = []
for x_temp in x_for_pred:
y_pred.append(model.coef_[0][0] * x_temp + model.intercept_[0])
plt.plot(x_for_pred, y_pred, color='red')
plt.xlim(3, 15)
plt.ylim(3, 12)
plt.show()
求めた回帰式を用いて予測を行う。
pred = model.predict(x)
pred
下記のような予測値が得られる。
array([[ 8.001 ],
[ 7.00081818],
[ 9.50127273],
[ 7.50090909],
[ 8.50109091],
[10.00136364],
[ 6.00063636],
[ 5.00045455],
[ 9.00118182],
[ 6.50072727],
[ 5.50054545]])
決定係数
上記で求めた予測値は、実測値との間に残差がある。
$$
1 = \frac{s_{予測}^2}{s_{実測}^2} + \frac{s_\epsilon^2}{s_{実測}^2}
$$
予測値平方和$s_{予測}^2$と実測値平方和$s_{実測}^2$の割合と、残差平方和$s_\epsilon^2$と実測値平方和$s_{実測}^2$の割合の和を求めると1になる。これは残差が実測値と予測値の差であるから自明といえる。
前者の割合が1に近づく(逆に後者の割合が0に近づく)方が、予測の精度は高いといえる。
この前者の割合(予測値平方和と実測値平方和の割合)を、寄与率もしくは決定係数という。
この値を求めるとき、予測値平方和および実測値平方和は偏差平方和としてする。
import numpy as np
# 偏差を求めるため平均値を求めておく
y_mean = np.mean(y)
p_mean = np.mean(pred)
ysos = 0 # 実測値の偏差平方和 y sum of squares
psos = 0 # 予測値の偏差平方和 pred sum of squares
rsos = 0 # 残差平方和 residual sum of squares
for i in range(0, len(y)):
ysos += (y_mean - y[i]) ** 2
psos += (p_mean - pred[i]) ** 2
residual = y[i] - pred[i]
rsos += residual ** 2
print('1になると正しい: %f' % (psos/ysos + rsos/ysos))
print('決定係数(R^2): %f' % (psos/ysos))
出力は下記のとおり。
1になると正しい: 1.000000
決定係数(R^2): 0.666542
決定係数は、scikit-learnを用いて下記のように求めることができる。
from sklearn.metrics import r2_score
print('決定係数(R^2): %f' % r2_score(y, pred))
print('決定係数(R^2): %f' % model.score(x, y))
出力される決定係数は、先に求めたものと同じである。
決定係数(R^2): 0.666542
決定係数(R^2): 0.666542
ところで、決定係数$R^2$は説明変数の数を増やすと(ここまででは説明変数が1つの単回帰分析を説明したが、説明変数が複数になると重回帰分析という)、大きな値になる性質がある。しかし、説明変数が増えれば必ずしも予測精度が高まるというわけではないため、その場合、決定係数は用いることができない。
自由度調整済み決定係数$\hat{R}^2$は、その問題に対応したものである。
$$
\hat{R}^2 = 1 – \frac{\frac{s_\epsilon^2}{N-p-1}}{\frac{s_{実測}^2}{N-1}}
$$
ここで、$N$はデータ数、$p$を説明変数の数とする。
scikit-learnでは自由度調整済み決定係数を求めることができないため、Pythonで下記のように計算する。
N = len(x) # データ数
p = 1 # 説明変数の数
print('自由度調整済み決定係数: %f' % (1 - (rsos/(N-p-1))/(ysos/(N-1))))
求められた自由度調整済み決定係数は、下記のとおり。
自由度調整済み決定係数: 0.629492
重回帰分析
bostonデータセットを用いて重回帰分析を行う。
from sklearn.datasets import load_boston
boston = load_boston()
print('data:', boston.data[0])
print('target:', boston.target[0])
print('feature_names:', boston.feature_names)
出力は下記のとおり。13個の説明変数があることが分かる。
data: [6.320e-03 1.800e+01 2.310e+00 0.000e+00 5.380e-01 6.575e+00 6.520e+01
4.090e+00 1.000e+00 2.960e+02 1.530e+01 3.969e+02 4.980e+00]
target: 24.0
feature_names: ['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
'B' 'LSTAT']
単回帰分析の場合と同様にscikit-learnを用いて重回帰分析を行う。
from sklearn import linear_model
# 線形回帰
model = linear_model.LinearRegression()
model.fit(boston.data, boston.target)
print('係数: %s' % model.coef_)
print('切片: %s' % model.intercept_)
係数: [-1.08011358e-01 4.64204584e-02 2.05586264e-02 2.68673382e+00
-1.77666112e+01 3.80986521e+00 6.92224640e-04 -1.47556685e+00
3.06049479e-01 -1.23345939e-02 -9.52747232e-01 9.31168327e-03
-5.24758378e-01]
切片: 36.459488385089855
下記のような回帰式を得られた。
$$
\hat{y} = -0.108x_{1}+0.046x_{2}+0.021x_{3}+2.687x_{4}+(-17.767)x_{5}\\+3.810x_{6}+0.001x_{7}+(-1.476)x_{8}+0.306x_{9}+(-0.012)x_{10}\\+(-0.953)x_{11}+0.009x_{12}+(-0.525)x_{13}+36.460
$$
決定係数を求める。
import numpy as np
# 予測値を得る
pred = model.predict(boston.data)
# 偏差を求めるため平均値を求めておく
y_mean = np.mean(boston.target)
p_mean = np.mean(pred)
ysos = 0 # 実測値の偏差平方和 y sum of squares
psos = 0 # 予測値の偏差平方和 pred sum of squares
rsos = 0 # 残差平方和 residual sum of squares
for i in range(0, len(boston.data)):
ysos += (y_mean - boston.target[i]) ** 2
psos += (p_mean - pred[i]) ** 2
residual = boston.target[i] - pred[i]
rsos += residual ** 2
print('1になると正しい: %f' % (psos/ysos + rsos/ysos))
print('決定係数(R^2): %f' % (psos/ysos))
N = len(boston.data) # データ数
p = len(boston.data[0]) # 説明変数の数
print('自由度調整済み決定係数: %f' % (1 - (rsos/(N-p-1))/(ysos/(N-1))))
1になると正しい: 1.000000
決定係数(R^2): 0.740643
自由度調整済み決定係数: 0.733790
偏回帰変数
bostonデータセットについて散布図行列を作成し、眺めてみる。
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['PRICE'] = boston.target
pd.plotting.scatter_matrix(df, figsize=(15,15), range_padding=0.2)
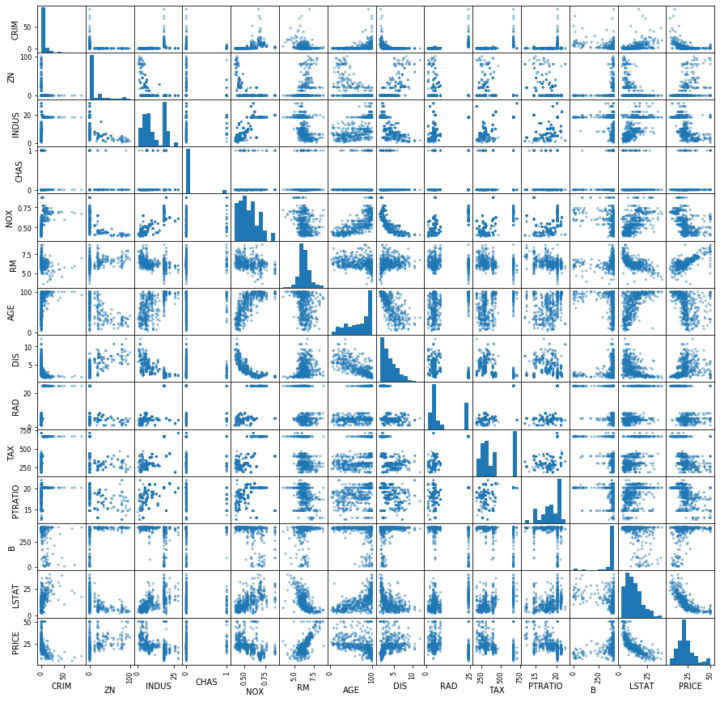
目的変数であるPRICEと、各説明変数との関係を見てみると、RMとの間に正の相関、LSTATとの間に負の相関が見える。この2つに絞って重回帰分析を再度行う。
x = df[['RM', 'LSTAT']].values
model = linear_model.LinearRegression()
model.fit(x, boston.target)
print('係数: %s' % model.coef_)
print('切片: %s' % model.intercept_)
print('決定係数(R^2): %f' % model.score(x, boston.target))
係数: [ 5.09478798 -0.64235833]
切片: -1.358272811874489
決定係数(R^2): 0.638562
以下の回帰式が得られた。
$$
\hat{y} = 5.095x_1 + (-0.642)x_2 + (-1.358)
$$
$x_1$はRM、$x_2$はLSTATを示すが、それぞれの係数である$5.095$と$-0.642$を偏回帰係数という。
RMが$1$増えるとPRICEは$5.095$上がり、LSTATが$1$増えるとPRICEは$0.642$下がることを示しているが、ここでRMとLSTATの関係について見る。
先ほど描いた散布図を見ると、負の相関が見て取れる。RMを目的変数$x_1$、LSTATを説明変数$x_2$として単回帰分析を行うと、下記のとおり。
x_1 = df['RM'].values
x_1 = x_1.reshape(-1, 1)
x_2 = df['LSTAT'].values
x_2 = x_2.reshape(-1, 1)
model = linear_model.LinearRegression()
model.fit(x_2, x_1)
print('係数: %s' % model.coef_)
print('切片: %s' % model.intercept_)
print('決定係数(R^2): %f' % model.score(x_2, x_1))
係数: [[-0.06039329]]
切片: [7.04879453]
決定係数(R^2): 0.376761
得られた回帰式は下記のとおり。
$$
\hat{x_1} = -0.060x_2 + 7.049
$$
LSTATが$1$増えると、RMは$-0.06$減ることを示している。この時、PRICEは$5.095\times(-0.06)$で$0.306$減ることになる。従って、LSTATが1増えると、$-0.642+(-0.306)$で$0.948$減る。
ここで、LSTATとPRICEについて回帰分析すると、下記のようになる。
x_2 = df['LSTAT'].values
x_2 = x_2.reshape(-1, 1)
model = linear_model.LinearRegression()
model.fit(x_2, boston.target)
print('係数: %s' % model.coef_)
print('切片: %s' % model.intercept_)
print('決定係数(R^2): %f' % model.score(x_2, boston.target))
係数: [-0.95004935]
切片: 34.55384087938311
決定係数(R^2): 0.544146
$$
\hat{y} = -0.950x_2 + 34.554
$$
この係数$-0.950$はLSTATが1増えたときにPRICEが増える(減る)割合を示すが、この値は先ほど得た値と近似している。
つまり、RMとLSTATを説明変数として用いた重回帰分析によって得たLSTATの偏回帰係数$-0.642$は、LSTATが増えたときにRMが増えた(減った)ことによってPRICEが増えた(減った)ことの影響を除外した目的変数への影響の割合ということになる。
多重共線性
再びすべての説明変数を用いて、変数間の相関係数を見る。
ここではヒートマップで見ることにする。
import seaborn as sns
sns.heatmap(df.corr())
RADとTAXの相関係数が極めて高くなっている。
df[['RAD', 'TAX']].corr()
RAD TAX
RAD 1.000000 0.910228
TAX 0.910228 1.000000
これは説明変数が他の説明変数から計算できるということであり、多重共線性が生じている可能性がある。重回帰分析を行う場合、相関が強い説明変数は含まないようにした方が良い。
