合成変数と主成分
bostonデータセットを用いた、主成分分析(PCA: Principal Components Analysis)を行う。
bostonデータセットには、13個の説明変数と、目的変数であるPRICEがある。
%matplotlib inline
from sklearn.datasets import load_boston
import pandas as pd
import matplotlib.pyplot as plt
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['PRICE'] = boston.target
pd.plotting.scatter_matrix(df, figsize=(15,15), range_padding=0.2)
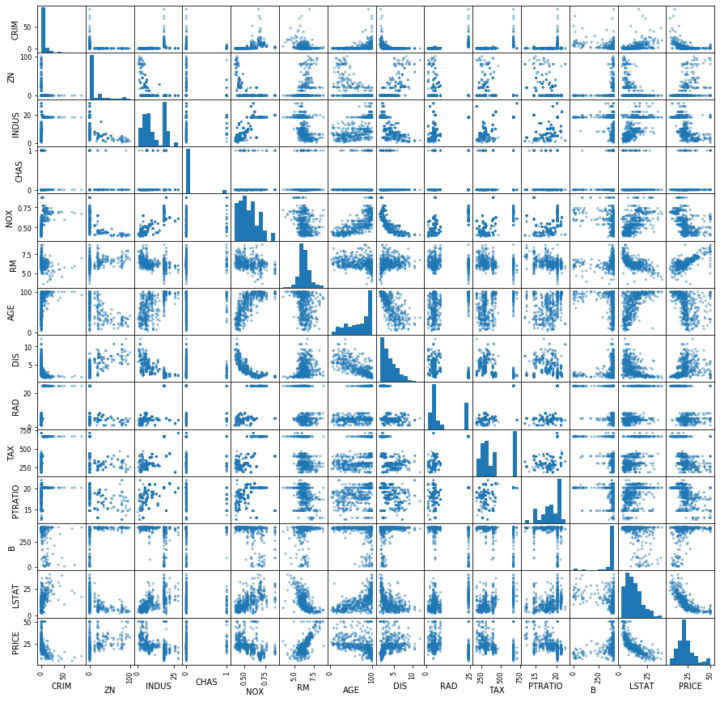
回帰分析の基礎で行ったように説明変数が13個あっても重回帰分析は可能だが、説明変数が増えると計算や可視化が複雑となり、また多重共線性の検討が必要となる。
そこで、データの特徴が残るように変数を合成し、合成変数を作る。この合成変数を主成分という。また、データの特徴を残すとは、データのばらつきが大きいということである。
そして、少数の合成変数でデータを表現できるようにしたい。これを主成分分析という。
scikit-learnで主成分分析を行う場合、下記のようにする。
事前にデータの標準化(平均が0、分散が1)をしておく必要がある。
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
x = boston.data
sc = StandardScaler()
x_sc = sc.fit_transform(x)
pca = PCA()
pca.fit(x_sc)
係数は固有ベクトルとして得られ、合成変数の分散は元の変数から作られる分散共分散行列の固有値となる。下記のように参照できる。
for i in range(0, len(pca.components_)):
print('Comp. %i' % (i+1))
print('固有ベクトル: %s' % pca.components_[i])
print('固有値: %s' % pca.explained_variance_[i])
sum = 0
for j in range(0, len(pca.components_[i])):
sum += pca.components_[i][j] ** 2
print('固有ベクトルの制約条件を満たすと1: %f' % sum)
Comp. 1
固有ベクトル: [ 0.2509514 -0.25631454 0.34667207 0.00504243 0.34285231 -0.18924257
0.3136706 -0.32154387 0.31979277 0.33846915 0.20494226 -0.20297261
0.30975984]
固有値: 6.138981200359455
固有ベクトルの制約条件を満たすと1: 1.000000
Comp. 2
固有ベクトル: [-0.31525237 -0.3233129 0.11249291 0.45482914 0.21911553 0.14933154
0.31197778 -0.34907 -0.27152094 -0.23945365 -0.30589695 0.23855944
-0.07432203]
固有値: 1.4361132907452232
固有ベクトルの制約条件を満たすと1: 1.000000
一つ目の主成分においては、下記の式が得られた。
$$
p = 0.251x_1+(-0.256)x_2+0.347x_3+0.005x_4+0.343x_5\\+(-0.189)x_6+0.314x_7+(-0.322)x_8+0.320x_9+0.338x_10\\+0.205x_11+(-0.203)x_12+0.310x_13
$$
数学的説明
例えば2つの変数$x_{1n}$と$x_{2n}$で合成変数$p_n$を作成する場合、下記のような計算を行う。
$$
p_n = w_1x_{1n} + w_2x_{2n} ・・・式1
$$
ここで、$p$の分散を最大にする係数$w_1$と$w_2$を求め、合成変数を作る。この係数はそれぞれの変数が合成変数にどの程度の影響を与えるかを示す。この合成変数を主成分という。
但し、係数の値を大きくすると、その分だけ分散が大きくなるため、下記の制約を設ける。
$$
w_1^2 + w_2^2 + \dots + w_m^2 = 1 ・・・式2
$$
合成変数$p$の分散$s_p^2$を求める式は下記のとおり。
$$
s_p^2 = \frac{(p_1-\bar{p})^2+(p_2-\bar{p})^2+\dots+(p_n-\bar{p})^2}{n} ・・・式3
$$
$\bar{p}$は合成変数$p$の平均値、$n$は合成変数の個数である。
ここに合成変数を求める式1を代入すると、下記のようになる。
$$
s_p^2 = w_1^2s_{x1}^2 + w_2^2s_{x2}^2 + 2w_1w_2s_{x1x2} ・・・式4
$$
$s_{x1}^2$と$s_{x2}^2$は変数$x_1$と$x_2$の分散を表し、$s_{x1x2}$は変数$x_1$と$x_2$の共分散を表す。
この合成変数の分散$s_p^2$を、式2の制約の下で最大化する係数$w_1$、$w_2$を求めるには、ラグランジュの未定数乗法を使う。
主成分の寄与率
ここで求めた主成分がどの程度、もとのデータの情報を表現しているかは寄与率として示される。
寄与率は、もとのデータでの変数の分散の和のうち、主成分の分散がどの程度の割合かによって求めることができる。
$$
主成分の寄与率 = \frac{主成分の分散}{もとのデータの変数の分散の和}
$$
寄与率が最も高い主成分を第1主成分、次を第2主成分のようにいう。また、第1主成分から順に寄与率を足し合わせたものを累積寄与率といい、一般的には累積寄与率が0.8になるまでの主成分を採用することが多い。
# 寄与率と累積寄与率
print('主成分', '寄与率', '累積寄与率')
comulative = 0.0
for i in range(0, len(pca.explained_variance_ratio_)):
comulative += pca.explained_variance_ratio_[i]
print('Comp. %i %f %f' % (i+1, pca.explained_variance_ratio_[i], comulative))
主成分 寄与率 累積寄与率
Comp. 1 0.471296 0.471296
Comp. 2 0.110252 0.581548
Comp. 3 0.095586 0.677134
Comp. 4 0.065967 0.743101
Comp. 5 0.064217 0.807318
Comp. 6 0.050570 0.857888
Comp. 7 0.041181 0.899069
Comp. 8 0.030469 0.929538
Comp. 9 0.021303 0.950841
Comp. 10 0.016941 0.967783
Comp. 11 0.014309 0.982091
Comp. 12 0.013023 0.995115
Comp. 13 0.004885 1.000000
bostonデータセットにおいては、累積寄与率が0.8に到達するには第5主成分までを採用する必要がある。
主成分負荷量
先ほど求めた主成分の式について、それぞれの変数の係数は、その主成分に寄与している度合いである。それぞれの変数の単位や分散が異なる場合、係数間の比較をすることができない。
そこで、主成分に対する元の変数の相関係数を求め、主成分負荷量(Principal Component Loading)とする。例えば、第1主成分$p$と第2主成分$q$があり、それが元の変数$x_1$と$x_2$の合成変数であった場合、$x_1$の主成分負荷量は第1主成分に対して$r_{px1}$、第2主成分に対して$r_{px2}$となる。ここで$r$は相関係数であることを示す。
また、係数(固有ベクトル)に標準偏差(固有値の平方根)を掛け合わせて求めることもできる。。
import numpy as np
import pandas as pd
features = []
for i in range(0, len(boston.feature_names)):
feature = [boston.feature_names[i]]
for j in range(2):
coef = pca.components_[j][i]
var = pca.explained_variance_[j]
loading = coef * np.sqrt(var)
feature.append(coef)
feature.append(loading)
features.append(feature)
df = pd.DataFrame(features, columns=['feature', 'coef1', 'loading1', 'coef2', 'loading2'])
df = df.set_index('feature')
print(df)
coef1 loading1 coef2 loading2
feature
CRIM 0.250951 0.621781 -0.315252 -0.377792
ZN -0.256315 -0.635070 -0.323313 -0.387452
INDUS 0.346672 0.858948 0.112493 0.134809
CHAS 0.005042 0.012494 0.454829 0.545058
NOX 0.342852 0.849484 0.219116 0.262584
RM -0.189243 -0.468886 0.149332 0.178956
AGE 0.313671 0.777181 0.311978 0.373868
DIS -0.321544 -0.796688 -0.349070 -0.418318
RAD 0.319793 0.792350 -0.271521 -0.325385
TAX 0.338469 0.838624 -0.239454 -0.286956
PTRATIO 0.204942 0.507785 -0.305897 -0.366581
B -0.202973 -0.502905 0.238559 0.285885
LSTAT 0.309760 0.767491 -0.074322 -0.089066
主成分負荷量をプロットする。
主成分負荷量の符号及び絶対値に基づき、主成分の意味付けを行うことができる。例えば、主成分負荷量の符号が同じ場合、総合的な評価を表すということができる。また、各変数の意味合いを合わせて検討する必要がある。
%matplotlib inline
import matplotlib.pyplot as plt
ax = plt.subplot()
for i in range(0, len(features)):
label = features[i][0][0:3]
loading1 = features[i][2]
loading2 = features[i][4]
ax.scatter(loading1, loading2, marker='$%s$' % label, s=1000)
ax.set_xlabel('Comp. 1')
ax.set_ylabel('Comp. 2')
ax.grid()
plt.show()
主成分得点
元のデータを主成分の軸に射影した軸上の値を主成分得点という。
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
x = boston.data
sc = StandardScaler()
x_sc = sc.fit_transform(x)
# 第2主成分までを使用
pca = PCA(n_components=2)
pca.fit(x_sc)
# データを射影する
x_projection = pca.transform(x_sc)
print(x_projection)
下記のように2軸に射影した値が得られる。
[[-2.09829748 0.77311539]
[-1.45725167 0.59198647]
[-2.07459756 0.59963956]
...
[-0.31236047 1.15524763]
[-0.27051907 1.04136268]
[-0.12580322 0.76197936]]
散布図を描く。
ax = plt.subplot()
for d in x_projection:
ax.scatter(d[0], d[1])
ax.grid()
ax.set_xlabel('Comp. 1')
ax.set_ylabel('Comp. 2')
plt.show()
