今週末に3時間ほど喋らないといけないのですが、いつもやっている研修というほどではなくて、何をテーマにしようかと考えています。
それで、機械学習について何か初歩的な話をしようということで、線形回帰の基本中の基本と、できれば単純パーセプトロンくらいの話ができれば良いかなと。
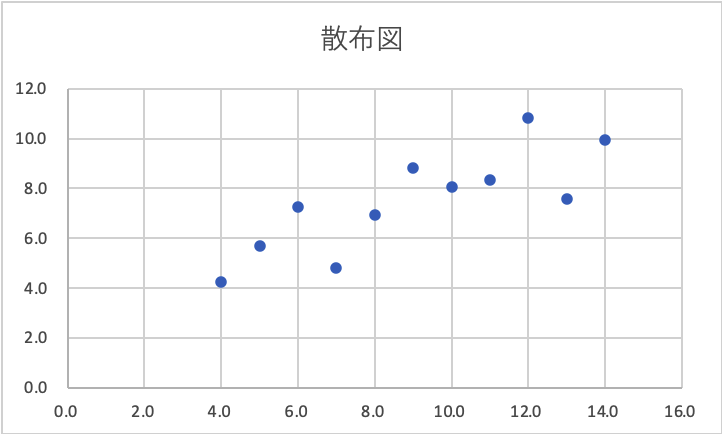
その例題として、線形回帰で使える典型的なデータセットとして、anscombeの1つ目を使うことにしました。
Excelで散布図を書くと、こんな感じになります。
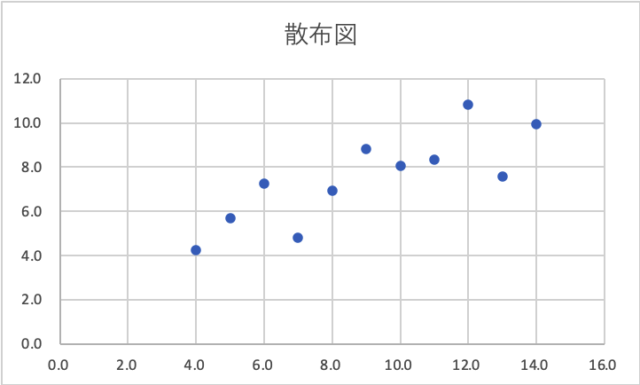
ついでに、Excelで傾きと切片を求めると、傾きが約0.5、切片が約3.0となります。Excelでは、SLOPE関数で傾きが、INTERCEPT関数で切片が求められるんですね。初めて知った。いままでは、Excelの分析ツール機能を使って線形回帰をやっていたので・・・。
求めた傾きと切片を使ってグラフを描くこと、こんな感じで、一本の線ができます。(線形回帰ですから。)
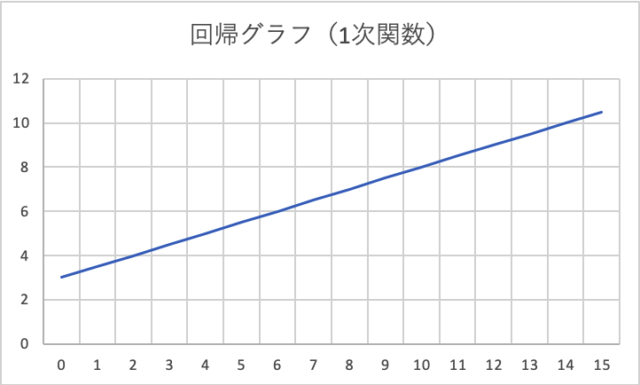
で、ここまでは良いのですが、せっかくなので傾きと切片を解析的に求めてみようではないかと。傾きを0.1〜1.0まで0.1刻みで、切片は2〜4まで1刻みにして、それぞれ平均二乗誤差を求めた場合、それが最小になるのは何か?と。
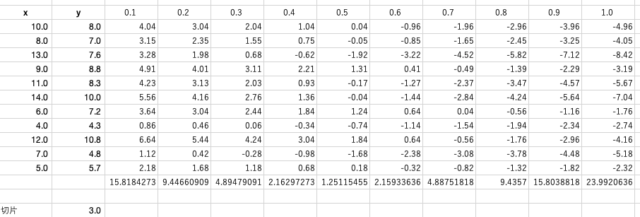
これは、切片が3の時の、それぞれの傾きでの平均二乗誤差ですが、ちゃんと傾きを0.5にしたときが最小になっていることが分かります。もちろん、切片を2と4で試した場合を含めても、傾きが0.5で切片が3の時の平均二乗誤差が最小になります。
切片が3の場合の平均二乗誤差をグラフにするとこうなります。
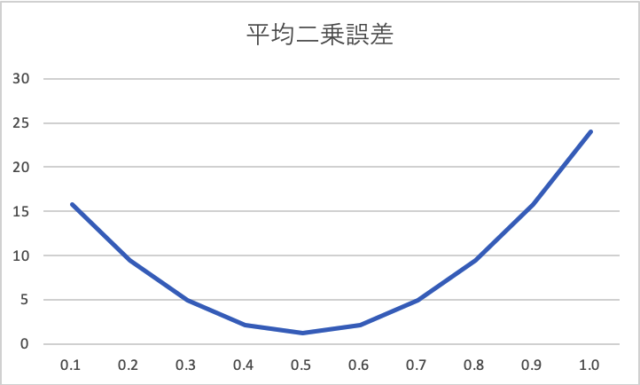
ざっと、これくらいの内容をゆっくりお話しして、単純パーセプトロンだと数式は活性化関数が入る以外は同じだよ・・・と持っていけば、ニューラルネットワークの基礎の内容にもなるし、良いかなと。多層パーセプトロンやディープラーニングの話までは進めませんが、あんまり盛り込みすぎるのも良くないし。
あと、今回使ったデータセットはanscombeの1つ目のやつだけだけど、もともとanscombeのデータセットは4種類あって、それぞれ回帰分析をやるとまったく同じ傾きと切片になるんですよね。だから、すぐに回帰分析やるんじゃなくて、まずは散布図とか見てみようねという戒め的なデータセット。
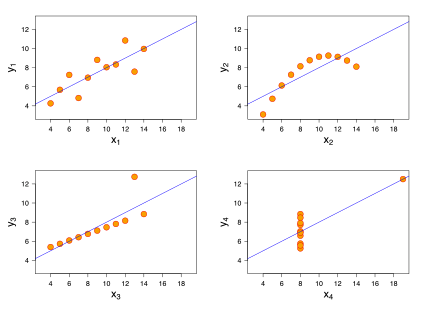
(出典:Wikipedia)
なので、できれば、そういう話もしたいなぁと思っています。